이 글은 이해한 것을 적어놓은 것이며, '한눈에 보이는 컴퓨터 구조'에서 가져왔다.
연산기 개요
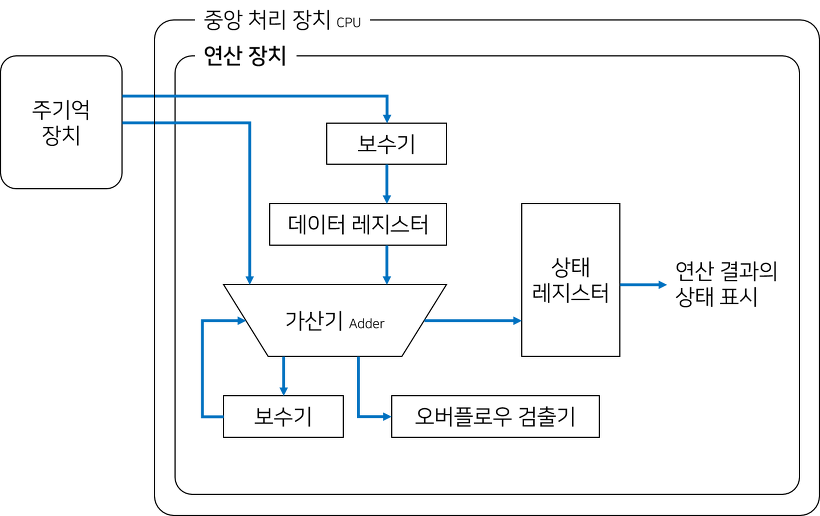
연산기
중앙처리장치 안에서 실제로 데이터에 대한 산술 및 논리 연산을 수행하는 부분
제어장치는 명령어를 해독하여 연산기에서 어떤 연산을 수행할지 결정하는 제어 신호를 생성한다.
연산의 종류를 계산에 사용되는 한의 수로 나누기도 한다.
- 단항 연산자 : -(음수 만들기), 1의 보수(NOT), 왼쪽/오른쪽 시프트, 증가, 감소
- 이항 연산자 : 사칙 연산(+,-,*,/), 논리 연산(AND, OR, XOR), 비교(compear test)
정수
컴퓨터는 모든 데이터를 기본적으로 2진수로 표현한다. 컴퓨터는 0과 1로 수와 관련된 모든 것을 표현하는데, 이 방법으로 소수점과 음수 부호를 표현할 수 없다.
컴퓨터가 처리할 수 있는 수는 다음과 같다.
- 부호 없는 수(unsigned number) : 0을 포함하여 양정수만을 표현
- 부호 있는 수(정수, signed number) : 0과 양수, 음수를 모두 표현
- 실수(real number) : 소수점을 포함하는 수를 표현. 컴퓨터는 부동소수점 수로 표현
이러한 표현을 하기 위해 컴퓨터는 정수 기준으로 부호화 크기, 1의 보수, 2의 보수에 의한 정수 표현 방법을 채택했다.
부호화 크기
데이터를 표현하는 n비트 단어의 가장 왼쪽 비트를 부호 비트로 사용한다.부호비트가 0이면 양수이고, 부호 비트가 1이면 음수를 의미한다. 나머지 n-1비트는 수의 크기를 나타낸다.
따라서 n비트로 표할 수 있는 수의 범위는 -(2^(n-1) - 1) ~ +(2^(n-1) - 1)까지 이다.
그러나 컴퓨터로 수를 처리할 떄는 2가지 문제가 있는데, 하나는 0이 2개(+0, -0)라는 점과 덧셈과 뺼셈을 계산하기 위하여 부호를 별도로 고려해야 한다는 점이다. 두 수의 부호가 같은지 다른지에 따라 계산 알고리즘이 달라져야 한다.
보수
서로 보호하는 수라는 의미이다. 임의의 R진법의 수에 N에 대한 보수는 (R-1)의 보수와 R의 보수 두 가지가 있다.
N의 R의 보수 = R^N - N (N != 0)
= 0 (N = 0)
N의 R-1의 보수 = R^N - R^M - N (N != 0)
= 0 (N = 0)
= R^N -1 -N (N != 0, M = 0)
여기서 R^N의 값은 진법 R과 관계 없이 항상 100..0(0이 N개)로 표현되는 수이다.
(R-1)의 보수와 R의 보수의 관계는 다음과 같다.
Cr = C(r-1) + 1
2진수의 경우 원래의 수 N에 대하여 1을 0으로 바꾸고 0을 1로 바꿈으로써 1의 보수를 구할 수 있으며, 2의 보수는 1의 보수를 구한 후 1을 더하여 구한다.
1의 보수는 변환이 쉽다는 편리성이 있으나, 1의 보수로 음수를 표현할 떄 0에 대한 표현이 000..0과 111..1로 두 가지라는 단점이 있다.
2의 보수
컴퓨터는 정수 표현의 표준 방법으로 2의 보수 방법을 채택하고 있다. 정수를 n비트로 표현 할 때, 가장 왼쪽 비트는 부호 비트이고, 나머지 부분은 수의 크기를 나타낸다.
양수는 부호 비트가 0이고, 수의 크기는 2진수로 표현되며, 부호를 포함한 수 전체를 2의 보수로 변환한 것을 음수 표현으로 사용한다.
n비트로 표현할 수 있는 정수의 범위는 -2^(n-1) ~ (2^(n-1) - 1)이다.
2의 보수 방법을 채택한 이유는 가산기 하나만으로 덧셈과 뺼셈을 계산할 수 있기 때문이다.
논리 연산
연산기는 기본적으로 레지스터 또는 기억장치에 저장되어 있는 데이터에 대하여 연산을 수행한다.
연산기는 논리 연산을 수행할 때 데이터를 부호없는 수로 취급한다.
기본적인 논리연산의 종류는 단항 논리 연산인 NOT과 이항 논리 연산인 AND, OR, XOR가 있다.
NOT연산
NOT 연산은 오퍼랜드의 각 비트에 대하여 논리 NOT 계산을 수행한다. 즉, 1을 0으로 0을 1로 바꾼다.
AND연산
두 개의 소스 오퍼랜드에 대하여 AND 연산을 수행하면,각 비트의 값이 둘 다 1인 비트는 1로 남고, 그렇지 않은 비트는 0으로 바뀐다.
데이터 비트 중에서 일부 비트만 남기고 나머지는 0으로 채우는 연산을 마스크 연산이라 하는데, AND연산을 유용하게 사용할 수 있다.
OR연산
두 개의 소스 오퍼랜드에 대하여 OR 연산을 수행하면, 비트 중 하나가 1인 비트는 1로, 둘 다 0인 비트는 0으로 리셋된다.
데이터 비트 중에서 일부 비트는 그대로 두고 특정 비트를 1로 세트하는 연산을 선택적 세트라고하는데, OR연산을 사용한다.
XOR연산
두 개의 소스 오퍼랜드에 대하여 XOR연산을 수행하면, 각 비트의 값이 서로 다르면 1로, 서로 같으면 0으로 리셋된다.
데이터 비트 중에서 일부 비트는 그대로 두고 특정 비트의 값을 반전시키는 선택적 보수를 수행하고자 할 떄, XOR 연산을 사용할 수 있다.
여러 비트에 대한 XOR 연산은 1의 수가 홀수이면 출력이 1이고, 짝수이면 출력이 0이 되는 성질을 갖고 패리티 검사를 할 때 사용한다. 이 때, XOR 연산 결과로 만들어진 데이터를 체크섬이라한다.
시프트 연산
데이터를 왼쪽 혹은 오른쪽으로 한 비트씩 자리 이동하는 연산이다.
종류는 논리 시프트(logical shift), 산술 시프트(arithmetic shift), 그리고 회전(rotate)이 있고, 각 연산에 대하여 자리 이동 방향에 따라 왼쪽, 오른쪽 두 가지 방법이 있다.
논리 시프트
오퍼랜드를 부호 없는 수로 취급한다.
- 왼쪽 논리 시프트 : 각 비트를 한 자리씩 왼쪽으로 이동한다. 최하위 비트(LSB)는 0으로 채워지고, 최상위 비트(MSB)는 상태 레지스터의 자리올림수 플래그(carry flag,C)에 저장된다.
- 오른쪽 논리 시프트 : 각 비트를 한 자리씩 오른쪽으로 이동한다. MSB는 0으로 채워지고, LSB는 상태 레지스터의 C에 저장된다.
산술 시프트
오퍼랜드를 부호 있는 수로 취급한다.
- 왼쪽 산술 시프트 : 부호 비트는 그대로 남고, 나머지 비트들이 한 자리씩 왼쪽으로 이동한다. 부호 비트를 제외한 MSB는 제거되고, LSB에 0이 채워진다.
- 오른쪽 산술 시프트 : 부호 비트는 그대로 남고, 나머지 비트들이 한 자리씩 오른쪽으로 이동한다. 부호 비트를 제외한 MSB자리에 부호 비트가 밀려 들어가고, LSB는 제거된다.
회전
시프트와 다르게 밀려 없어지는 비트가 반대 방향의 끝으로 채워지는 연산이다.
오퍼랜드를 부호 없는 수로 취급한다.
정수 산술 연산
연산기는 부호 없는 수 혹은 정수(부호 있는 수)에 대하여 산술 연산(arithmetic operation)을 수행한다.
단항 연산
종류는 2의 보수화(부호 변경), 증가, 감소의 세 가지가 있다.
덧셈과 뺄셈
정수를 2의 보수로 표현하기 떄문에, 곱하기와 나누기를 제외한 산술 연산은 오퍼랜드의 값이 부호 없는 수인지 혹은 부호 있는 수인지를 고려할 필요가 없어진다. 그 수를 부호 없는 수로 해석할지 정수로 해석할지는 사람의 몫이다.
컴퓨터에서는 덧셈을 계산할 떄, 레지스터의 크기가 제한되어 있기 때문에 계산 결과가 틀려지는 경우가 발생하는 데, 이러한 현상을 오버플로우(overflow)라고 부른다.
곱셈
크기가 n비트인 두 개의 정수 A와 B를 곱하면 그 결과는 2n비트이다.
곱셈 A*B를 수행한다고 할 때, A를 피승수(multiplicand), B를 승수(multiplier), 그리고 곱셈 결과를 곱(product)이라고 한다.
n비트의 병렬 덧셈기를 n번 반복 사용하여 곱을 구할 수 있다.
나눗셈
크기가 2n비트인 피젯수(dividend)를 크기가 n비트인 젯수(divisor)로 나누면, 크기가 n비트인 몫(quotient)과 크기가 n비트인 나머지(remainder)가 생성된다.
실수
컴퓨터는 실수를 부동소수점 수(floating-point number)로 표현한다.
부동소수점 표현
실수를 부호(sign), 가수(mantissa,significant, or fraction), 기수(base),그리고 지수(exponent)로 표시한다.
- 97,600,000,000 = 9.76 * 10^10 부호 : +, 가수 : 9.76, 기수 : 10, 지수 : 10
- 0.00000000000976 = -9.76 * 10^-12 부호 : -, 가수 : 9.76, 기수 : 10, 지수 : -12
기수에 포함된 소수점의 위치를 변경하면서 이에 따라 지수를 조정할 수 있으므로 이 방법을 부동소수점 표현이라고 부른다.
IEEE 754 형식
'컴퓨터구조' 카테고리의 다른 글
| 컴퓨터구조_09.기억장치 (0) | 2021.12.15 |
|---|---|
| 컴퓨터구조_08.제어장치 (0) | 2021.12.15 |
| 컴퓨터구조_07.중앙처리장치 설계 (0) | 2021.12.14 |
| 컴퓨터구조_04.중앙처리장치 (1) | 2021.10.05 |